Universal vertex

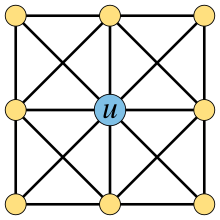
In graph theory, a universal vertex is a vertex of an undirected graph that is adjacent to all other vertices of the graph. It may also be called a dominating vertex, as it forms a one-element dominating set in the graph. (It is not to be confused with a universally quantified vertex in the logic of graphs.)

A graph that contains a universal vertex may be called a cone. In this context, the universal vertex may also be called the apex of the cone.^[1] However, this terminology conflicts with the terminology of apex graphs, in which an apex is a vertex whose removal leaves a planar subgraph.

In special families of graphs[edit]

The stars are exactly the trees that have a universal vertex, and may be constructed by adding a universal vertex to an independent set. The wheel graphs, similarly, may be formed by adding a universal vertex to a cycle graph.^[2] The trivially perfect graphs (the comparability graphs of order-theoretic trees) always contain a universal vertex, the root of the tree, and more strongly they may be characterized as the graphs in which every connected induced subgraph contains a universal vertex.^[3] The connected threshold graphs form a subclass of the trivially perfect graphs, so they also contain a universal vertex; they may be defined as the graphs that can be formed by repeated addition of either a universal vertex or an isolated vertex (one with no incident edges).^[4]

In geometry, the three-dimensional pyramids have wheel graphs as their skeletons,^[5] and more generally a higher-dimensional pyramid is a polytope whose faces of all dimensions connect an apex vertex to all the faces of a lower-dimensional base, including all of the vertices of the base. The polytope is said to be pyramidal at its apex, and it may have more than one apex. However, the existence of neighborly polytopes means that the graph of a polytope may have a universal vertex, or all vertices universal, without the polytope itself being a pyramid.^[6]

The friendship theorem of Paul Erdős, Alfréd Rényi, and Vera T. Sós (1966) states that, if every two vertices in a finite graph have exactly one shared neighbor, then the graph contains a universal vertex. The graphs described by this theorem are the friendship graphs, formed by systems of triangles connected together at a common shared vertex, the universal vertex.^[7] The assumption that the graph is finite is important; there exist infinite graphs in which every two vertices have one shared neighbor, but with no universal vertex.^[8]

Every graph with a universal vertex is a dismantlable graph, meaning that it can be reduced to a single vertex by repeatedly removing vertices whose closed neighborhoods are subsets of other vertices' closed neighborhoods. Any removal sequence that leaves the universal vertex in place, removing all of the other vertices, fits this definition. Almost all dismantlable graphs have a universal vertex, in the sense that the fraction of $n$ -vertex dismantlable graphs that have a universal vertex tends to one in the limit as $n$ goes to infinity.^[9]

When a graph has a universal vertex, the vertex set consisting only of that vertex is a dominating set, a set that includes or is adjacent to every vertex. For this reason, in the context of dominating set problems, a universal vertex may also be called a dominating vertex.^[10] For the strong product of graphs $G\boxtimes H$ , the domination numbers $\gamma (G)$ and $\gamma (H)$ obey the inequalities

\max\{\gamma (G),\gamma (H)\}\leq \gamma (G\boxtimes H)\leq \gamma (G)\gamma (H).

This implies that a strong product has a dominating vertex if and only if both of its factors do; in this case the upper bound on its dominating number is one, and in any other case the lower bound is greater than one.^[11]

Recognition[edit]

In a graph with $n$ vertices, a universal vertex is a vertex whose degree is exactly $n - 1$ .^[10]

The property of having a universal vertex can be expressed by a formula in the first-order logic of graphs. Using $\sim$ to indicate the adjacency relation in a graph, a graph $G$ has a universal vertex if and only if it models the formula

\exists u\forall v{\bigl (}(u\neq v)\Rightarrow (u\sim v){\bigr )}.

The existence of this formula, and its small number of alternations between universal and existential quantifers, can be used in a fixed-parameter tractable algorithm for testing whether all components of a graph can be made to have universal vertices by

k

steps of removing a vertex from each component.^[12]

References[edit]

^ Larrión, F.; de Mello, C. P.; Morgana, A.; Neumann-Lara, V.; Pizaña, M. A. (2004), "The clique operator on cographs and serial graphs", Discrete Mathematics, 282 (1–3): 183–191, doi:10.1016/j.disc.2003.10.023, MR 2059518.
^ Bonato, Anthony (2008), A course on the web graph, Graduate Studies in Mathematics, vol. 89, Atlantic Association for Research in the Mathematical Sciences (AARMS), Halifax, NS, p. 7, doi:10.1090/gsm/089, ISBN 978-0-8218-4467-0, MR 2389013.
^ Wolk, E. S. (1962), "The comparability graph of a tree", Proceedings of the American Mathematical Society, 13 (5): 789–795, doi:10.2307/2034179, JSTOR 2034179, MR 0172273.
^ Chvátal, Václav; Hammer, Peter Ladislaw (1977), "Aggregation of inequalities in integer programming", in Hammer, P. L.; Johnson, E. L.; Korte, B. H.; Nemhauser, G. L. (eds.), Studies in Integer Programming (Proc. Worksh. Bonn 1975), Annals of Discrete Mathematics, vol. 1, Amsterdam: North-Holland, pp. 145–162.
^ Pisanski, Tomaž; Servatius, Brigitte (2013), Configuration from a Graphical Viewpoint, Springer, p. 21, doi:10.1007/978-0-8176-8364-1, ISBN 978-0-8176-8363-4
^ Klee, Victor (1964), "On the number of vertices of a convex polytope", Canadian Journal of Mathematics, 16: 701–720, doi:10.4153/CJM-1964-067-6, MR 0166682
^ Erdős, Paul; Rényi, Alfréd; Sós, Vera T. (1966), "On a problem of graph theory" (PDF), Studia Sci. Math. Hungar., 1: 215–235.
^ Chvátal, Václav; Kotzig, Anton; Rosenberg, Ivo G.; Davies, Roy O. (1976), "There are $\scriptstyle 2^{\aleph _{\alpha }}$ friendship graphs of cardinal $\scriptstyle \aleph _{\alpha }$ ", Canadian Mathematical Bulletin, 19 (4): 431–433, doi:10.4153/cmb-1976-064-1.
^ Bonato, Anthony; Kemkes, Graeme; Prałat, Paweł (2012), "Almost all cop-win graphs contain a universal vertex", Discrete Mathematics, 312 (10): 1652–1657, doi:10.1016/j.disc.2012.02.018, MR 2901161.
^ ^a ^b Haynes, Teresa W.; Hedetniemi, Stephen T.; Henning, Michael A. (2023), Domination in Graphs: Core Concepts, Springer Monographs in Mathematics, Springer, Cham, p. 2, doi:10.1007/978-3-031-09496-5, ISBN 978-3-031-09495-8, MR 4607811
^ Fisher, David C. (1994), "Domination, fractional domination, 2-packing, and graph products", SIAM Journal on Discrete Mathematics, 7 (3): 493–498, doi:10.1137/S0895480191217806, MR 1285586
^ Fomin, Fedor V.; Golovach, Petr A.; Thilikos, Dimitrios M. (2021), "Parameterized complexity of elimination distance to first-order logic properties", 36th Annual ACM/IEEE Symposium on Logic in Computer Science, LICS 2021, Rome, Italy, June 29 - July 2, 2021, IEEE, pp. 1–13, arXiv:2104.02998, doi:10.1109/LICS52264.2021.9470540, S2CID 233169117

[1] Larrión, F.; de Mello, C. P.; Morgana, A.; Neumann-Lara, V.; Pizaña, M. A. (2004), "The clique operator on cographs and serial graphs", Discrete Mathematics, 282 (1–3): 183–191, doi:10.1016/j.disc.2003.10.023, MR 2059518.

[2] Bonato, Anthony (2008), A course on the web graph, Graduate Studies in Mathematics, vol. 89, Atlantic Association for Research in the Mathematical Sciences (AARMS), Halifax, NS, p. 7, doi:10.1090/gsm/089, ISBN 978-0-8218-4467-0, MR 2389013.

[3] Wolk, E. S. (1962), "The comparability graph of a tree", Proceedings of the American Mathematical Society, 13 (5): 789–795, doi:10.2307/2034179, JSTOR 2034179, MR 0172273.

[4] Chvátal, Václav; Hammer, Peter Ladislaw (1977), "Aggregation of inequalities in integer programming", in Hammer, P. L.; Johnson, E. L.; Korte, B. H.; Nemhauser, G. L. (eds.), Studies in Integer Programming (Proc. Worksh. Bonn 1975), Annals of Discrete Mathematics, vol. 1, Amsterdam: North-Holland, pp. 145–162.

[5] Pisanski, Tomaž; Servatius, Brigitte (2013), Configuration from a Graphical Viewpoint, Springer, p. 21, doi:10.1007/978-0-8176-8364-1, ISBN 978-0-8176-8363-4

[6] Klee, Victor (1964), "On the number of vertices of a convex polytope", Canadian Journal of Mathematics, 16: 701–720, doi:10.4153/CJM-1964-067-6, MR 0166682

[7] Erdős, Paul; Rényi, Alfréd; Sós, Vera T. (1966), "On a problem of graph theory" (PDF), Studia Sci. Math. Hungar., 1: 215–235.

[8] Chvátal, Václav; Kotzig, Anton; Rosenberg, Ivo G.; Davies, Roy O. (1976), "There are $\scriptstyle 2^{\aleph _{\alpha }}$ friendship graphs of cardinal $\scriptstyle \aleph _{\alpha }$ ", Canadian Mathematical Bulletin, 19 (4): 431–433, doi:10.4153/cmb-1976-064-1.

[9] Bonato, Anthony; Kemkes, Graeme; Prałat, Paweł (2012), "Almost all cop-win graphs contain a universal vertex", Discrete Mathematics, 312 (10): 1652–1657, doi:10.1016/j.disc.2012.02.018, MR 2901161.

[h3-10] Haynes, Teresa W.; Hedetniemi, Stephen T.; Henning, Michael A. (2023), Domination in Graphs: Core Concepts, Springer Monographs in Mathematics, Springer, Cham, p. 2, doi:10.1007/978-3-031-09496-5, ISBN 978-3-031-09495-8, MR 4607811

[11] Fisher, David C. (1994), "Domination, fractional domination, 2-packing, and graph products", SIAM Journal on Discrete Mathematics, 7 (3): 493–498, doi:10.1137/S0895480191217806, MR 1285586

[12] Fomin, Fedor V.; Golovach, Petr A.; Thilikos, Dimitrios M. (2021), "Parameterized complexity of elimination distance to first-order logic properties", 36th Annual ACM/IEEE Symposium on Logic in Computer Science, LICS 2021, Rome, Italy, June 29 - July 2, 2021, IEEE, pp. 1–13, arXiv:2104.02998, doi:10.1109/LICS52264.2021.9470540, S2CID 233169117

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]