Brandes' algorithm

Brandes' algorithm

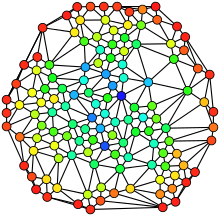An undirected graph colored based on the betweenness centrality of each vertex from least (red) to greatest (blue).
Class	Centrality Network theory
Data structure	Connected graph
Worst-case performance	$O(|V||E|)$ (unweighted) $O(|V||E|+|V|^{2}\log |V|)$ (weighted)
Worst-case space complexity	$O(|V|+|E|)$

In network theory, Brandes' algorithm is an algorithm for calculating the betweenness centrality of vertices in a graph. The algorithm was first published in 2001 by Ulrik Brandes. Betweenness centrality, along with other measures of centrality, is an important measure in many real-world networks, such as social networks and computer networks.

Definitions

There are several metrics for the centrality of a node, one such metric being the betweenness centrality. For a node $v$ in a connected graph, the betweenness centrality is defined as:

$C_{B}(v)=\sum _{s\in V}\sum _{t\in V}{\frac {\sigma _{st}(v)}{\sigma _{st}}}$

where $\sigma _{st}$ is the total number of shortest paths from node $s$ to node $t$, and $\sigma _{st}(v)$ is the number of these paths which pass through $v$. For an unweighted graph, the length of a path is considered to be the number of edges it contains.

By convention, $\sigma _{st}=1$ whenever $s=t$, since the only path is the empty path. Also, $\sigma _{st}(v)=0$ if $v$ is either $s$ or $t$, since shortest paths are considered not to have truly passed through their endpoints.

The quantity

$\delta _{st}(v)={\frac {\sigma _{st}(v)}{\sigma _{st}}}$

is known as the pair dependency on $v$, and represents the proportion of the shortest $s$–$t$ paths which travel via $v$. The betweenness centrality is simply the sum of the pair dependencies over all pairs. As well as the pair dependency, it is also useful to define the (single) dependency on $v$ , with respect to a particular vertex $s$:

$\delta _{s}(v)=\sum _{t\in V}\delta _{st}(v)$,

with which, we can obtain the concise formulation

$C_{B}(v)=\sum _{s\in V}\delta _{s}(v)$.

Algorithm

Brandes' algorithm calculates the betweenness centrality of all nodes in a graph. For every vertex $s$, there are two stages.

1. Single-source shortest path

The number of shortest paths $\sigma _{sv}$ between $s$ and every vertex $v$ is calculated using breadth-first search. The breadth-first search starts at $s$, and the shortest distance $d(v)$ of each vertex from $s$ is recorded, dividing the graph into discrete layers. Additionally, each vertex $v$ keeps track of the set of vertices which in the preceding layer which point to it, $p(v)$. Described in set-builder notation, it can be written as:

$p(v)=\{u\in V\mid (u,v)\in E\land d(u)+1=d(v)\}$.

This lends itself to a simple iterative formula for $\sigma _{sv}$:

$\sigma _{sv}=\sum _{u\in p(v)}\sigma _{su}$,

which essentially states that, if $v$ is at depth $d(v)$, then any shortest path at depth $d(v)-1$ extended by a single edge to $v$ becomes a shortest path to $v$.

2. Backpropagation

Brandes proved the following recursive formula for vertex dependencies:

$\delta _{s}(u)=\sum _{v\mid u\in p(v)}{\frac {\sigma _{su}}{\sigma _{sv}}}\cdot (1+\delta _{s}(v))$,

where the sum is taken over all vertices $v$ that are one edge further away from $s$ than $u$. This lemma eliminates the need to explicitly sum all of the pair dependencies. Using this formula, the single dependency of $s$ on a vertex $u$ at depth $d(u)$ is determined by the layer at depth $d(u)+1$. Furthermore, the order of summation is irrelevant, which allows for a bottom up approach starting at the deepest layer.

It turns out that the dependencies of $s$ on all other vertices $u$ can be computed in $O(|E|)$ time. During the breadth-first search, the order in which vertices are visited is logged in a stack data structure. The backpropagation step then repeatedly pops off vertices, which are naturally sorted by their distance from $s$, descending.

For each popped node $v$, we iterate over its predecessors $u\in p(v)$: the contribution of $v$ towards $\delta _{s}(u)$ is added, that is,

${\frac {\sigma _{su}}{\sigma _{sv}}}\cdot (1+\delta _{s}(v))$.

Crucially, every layer propagates its dependencies completely, before moving to the layer with lower depth, due to the nature of breadth-first search. Once the propagation reaches back to $s$, every vertex $v$ now contains $\delta _{s}(v)$. These can simply be added to $C_{B}(v)$, since

$C_{B}(v)=\sum _{s\in V}\delta _{s}(v)$.

After $|V|$ iterations of single-source shortest path and backpropagation, each $C_{B}(v)$ contains the betweenness centrality for $v$.

Pseudocode

The following pseudocode illustrates Brandes' algorithm on an unweighted graph.

algorithm Brandes(Graph) is
    for each u in Graph.Vertices do
        CB[u] ← 0

    for each s in Graph.Vertices do
        for each v in Graph.Vertices do
            δ[v] ← 0                   // Single dependency of s on v
            prev[v] ← empty list       // Immediate predecessors of v during BFS
            σ[v] ← 0                   // Number of shortest paths from s to v (s implied)
            dist[v] ← null             // No paths are known initially,
        σ[s] ← 1                       // except the start vertex
        dist[s] ← 0

        Q ← queue containing only s    // Breadth-first search
        S ← empty stack                // Record the order in which vertices are visited

        // Single-source shortest paths

        while Q is not empty do
            u ← Q.dequeue()
            S.push(u)

            for each v in Graph.Neighbours[u] do
                if dist[v] = null then
                    dist[v] ← dist[u] + 1
                    Q.enqueue(v)
                if dist[v] = dist[u] + 1 then
                    σ[v] ← σ[v] + σ[u]
                    prev[v].append(u)

        // Backpropagation of dependencies

        while S is not empty do
            v ← S.pop()

            for each u in prev[v] do
                δ[u] ← δ[u] + σ[u] / σ[v] * (1 + δ[v])

                if u ≠ s then
                    CB[v] ← CB[v] + δ[v]

    return CB

Running time

The running time of the algorithm is expressed in terms of the number of vertices $|V|$ and the number of edges $|E|$.

For each vertex $s$, we run a breadth-first search, which takes $O(|V|+|E|)$ time. Since the graph is connected, the $|E|$ component subsumes the $|V|$ term, since the number of edges is at least $|V|-1$.

In the backpropagation stage, every vertex is popped off the stack, and its predecessors are iterated over. However, since each predecessor entry corresponds to an edge in the graph, and vice versa, this stage is also bounded by $O(|E|)$.

The overall running time of the algorithm is therefore $O(|V||E|)$. This is an improvement on the $O(|V|^{3})$ time bounds achieved by prior algorithms. The improvement can be attributed to the fact that the dependency on a vertex can be calculated from just its neighbours that are one level deeper. In addition, Brandes' algorithm improves on the space complexity of naive algorithms, which typically require $O(|V|^{2})$ space. Brandes' algorithm only stores at most $|E|$ predecessors, along with data for each vertex, making its extra space complexity $O(|V|+|E|)$

Variants

The algorithm can be generalised to weighted graphs, by using Dijkstra's algorithm instead of breadth-first search. When operating on undirected graphs, the betweenness centrality may be divided by 2, to avoid double counting each path's reversed counterpart. Variants also exist to calculate different measures of centrality, including betweenness with paths at most length $k$, edge betweenness, load betweenness, and stress betweenness.